VECTORS
Vector Basics
 Force is one of many things that are vectors.
Force is one of many things that are vectors. What the heck is a vector?
- Can you hold it? No.
- Can you watch it? No.
- Does it do anything? Well, not really.
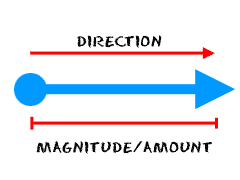
The force vector describes a specific amount of force and its direction.
- You need both value and direction to have a vector. Both. Very important. Scientists refer to the two values as direction and magnitude (size).
- The alternative to a vector is a scalar. Scalars have values, but no direction is needed. Temperature, mass, and energy are examples of scalars.
When you see vectors drawn in physics, they are drawn as arrows.
- The direction of the arrow is the direction of the vector
- the length of the arrow depends on the magnitude (size) of the vector.
Real World Vectors
 Imagine a situation where you're in a boat or a plane, and you need to plot a course. There aren't streets or signs along the way. You will need to plan your navigation on a map. You know where you're starting and where you want to be. The problem is how to get there. Now it's time to use a couple of vectors.
Imagine a situation where you're in a boat or a plane, and you need to plot a course. There aren't streets or signs along the way. You will need to plan your navigation on a map. You know where you're starting and where you want to be. The problem is how to get there. Now it's time to use a couple of vectors. Draw the vector between the two points and start on your way. As you move along your course, you will probably swerve a bit off course because of wind or water currents. Just go back to the map, find your current location, and plot a new vector that will take you to your destination. Captains use vectors (they know the speed and direction) to plot their courses.